Worthäufigkeiten als Hyperbel: Forscher haben eine weitere mathematische Gesetzmäßigkeit in literarischen Werken entdeckt. Wie oft ein Wort im Text auftaucht und in welchem Verhältnis es zum nächsthäufigen steht, lässt sich demnach mit einer verblüffend einfachen Formel ausdrücken. Übereinstimmungen mit diesem Zipfschen Gesetz fanden die Wissenschaftler immerhin in knapp der Hälfte der gut 30.000 englischsprachigen Werke im Projekt Gutenberg.
Dass sich in Literatur durchaus mathematische Prinzipien verstecken können, hat erst vor kurzem die Entdeckung von fraktalen Strukturen in großen Werken der Weltliteratur bewiesen. Aber es gibt noch viel vordergründigere Mathematik in geschriebenen Texten: das Zipfsche Gesetz. Diese 1930 vom US-Linguisten George Zipf aufgestellte Regel besagt, dass die Häufigkeit bestimmter Wörter in einem Text einer verblüffend simplen mathematischen Funktion folgt.
Worthäufigkeit als Hyperbel
Nach dem Zipfschen Gesetz entspricht die Verteilung der Worthäufigkeiten dabei in ihrer einfachsten Form einer Hyperbel mit der Formel 1/n. Konkret gesagt: Das häufigste Wort in einem Text kommt genau doppelt so oft vor wie das zweithäufigste, dieses wiederum ist ein dreimal häufiger als das drittplatzierte und so weiter. Für einzelne Werke wie beispielsweise den Roman Effi Briest von Fontane haben Analysen diesen Zusammenhang auch schon bestätigt.
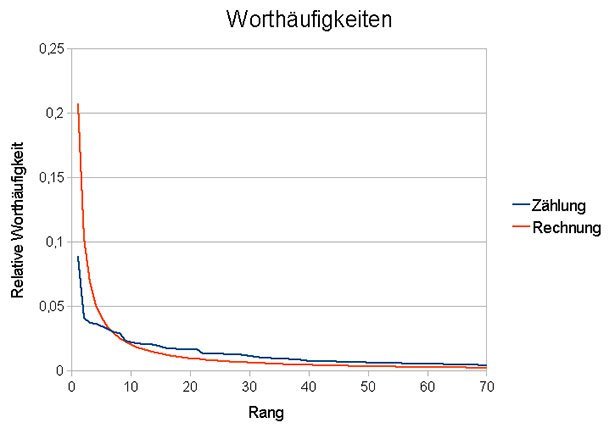
Aber gilt das Zipfsche Gesetz für alle literarischen Werke? Um das herauszufinden, haben Forscher der Universität Autònoma de Barcelona erstmals alle englischsprachigen Werke im Gutenberg-Projekt auf ihre Übereinstimmung mit drei Varianten dieses mathematischen Gesetzes untersucht. 30.000 Werke, und damit so viel wie noch nie zuvor, testeten die Wissenschaftler dafür.
