Nach 400 Jahren endlich formell bewiesen: Wie sich Kugeln am dichtesten packen lassen, beschrieb der Astronom Johannes Kepler schon im Jahr 1611. Doch den vollständigen formellen Beweis dafür, dass seine Vermutung auch für alle denkbaren Kugelmengen und Raumgrößen gilt, lieferten Mathematiker erst 1998. Dieser Beweis war jedoch so komplex, dass menschliche Gutachter an ihre Grenze stießen. Erst jetzt haben Computerprogramme die Gültigkeit dieses Beweises bestätigt.
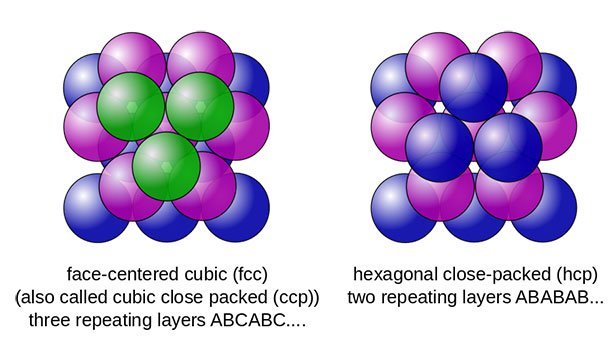
Die Keplersche Vermutung ist ein Klassiker der Geometrie: Es geht um die Frage, wie sich Kugeln am dichtesten in einem begrenzten Raum stapeln lassen – beispielsweise Orangen in einer Kiste. Intuitiv ist die Lösung einfach – und auch einfach auszuprobieren: Am wenigsten Raum nehmen die Kugeln ein, wenn sie pyramidenförmig – und damit beispielsweise kubisch-flächenzentriert oder hexagonal – gestapelt werden: Jede Kugel liegt in den Lücken der darunterliegenden Schicht.
Diese Lösung erkannte schon im Jahr 1611 der Astronom und Mathematiker Johannes Kepler. Ihm zufolge erreicht man mit dieser optimalen Stapelung eine Dichte von rund 74 Prozent. Doch das Problem war der mathematische Beweis: Dieser muss die Keplersche Vermutung für alle möglichen Raumgrößen und Kugelanordnungen mathematisch herleiten und belegen. Daran jedoch scheiterten Mathematiker Jahrhunderte lang.
Endlich ein Beweis – oder doch nicht?
1998 dann legte Thomas Hales von der University of Pittsburgh den lange gesuchten Beweis vor. Er hatte mit Hilfe eines Computerprogramms 5.000 verschiedene Kugelanordnungen durchgerechnet und für alle die Gültigkeit von Keplers Vermutung bewiesen. Das Problem dabei: Die Berechnungen dafür waren tausende Scriptzeilen lang und füllten ausgedruckt 250 Seiten.