„Kurzsichtige“ Software knackt komplexe Probleme

Wie viele unterschiedliche Sudokus gibt es? Auf wie viele verschiedene Weisen lassen sich die Länder auf einer Landkarte einfärben? Und wie verhalten sich die Atome in einem Festkörper? Bisher waren komplexere Fragen dieser Art unlösbar, da sie zu viel Rechenzeit brauchten. Doch jetzt haben Forscher einen neuartigewn Algorithmus entwickelt, der diese Probleme in Rekordzeit knackt.

In der neuen Methode schauen die Wissenschaftler nur einzelne Ausschnitte des Problems an und arbeiten diese nacheinander ab. Bislang hatten sie in jedem Rechenschritt etwa die gesamte Landkarte oder das gesamte Sudoku im Blick. Viele Fragestellungen aus Physik, Mathematik und Informatik lassen sich so erstmals beantworten. Die neue Methode wurde jetzt in der Fachzeitschrift „New Journal of Physics“ vorgestellt.

Wie viele „Farben“ gibt es?

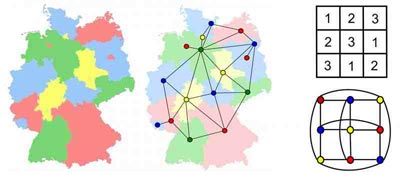
Ob Sudoku, Deutschlandkarte oder Festkörper – in allen Fällen geht es darum, Möglichkeiten zu zählen. Beim Sudoku sind es die erlaubten Lösungen, beim Festkörper die möglichen Anordnungen der Atome. Und im Fall der Landkarte stellt sich die Frage, auf wie viele Weisen sich die Karte einfärben lässt, so dass benachbarte Länder stets verschiedene Farben tragen. Abzähl-Probleme dieser Art stellen Wissenschaftler als Netz aus Linien und Knoten dar.

Beantworten müssen die Forscher dann nur eine Frage: Auf wie viele Weisen lassen sich die Knoten einfärben, wenn eine bestimmte Anzahl von Farben vorgegeben ist? Einzige Bedingung: Knoten, die durch eine Linie verbunden sind, dürfen nicht dieselbe Farbe haben. Je nach Anwendung kommt der „Farbe“ eines Knotens dabei eine völlig andere Bedeutung zu. Im Fall der Landkarte ist mit „Farbe“ tatsächlich die Farbe gemeint, beim Sudoku entsprechen den „Farben“ verschiedene Ziffern.

Eine Deutschlandkarte mit der entsprechenden Darstellung als Netz. Rechts oben: Ein vereinfachtes Sudoku aus drei mal drei Kästchen ("Magisches Quadrat"). Rechts unten: Die entsprechende Darstellung als Netz. Die "1" entspricht "rot", "2" entspricht "blau" und "3" entspricht "gelb". © MPIDS

Milliarden Jahre Rechenzeit

„Der bisherige Algorithmus kopiert bei jedem Rechenschritt das gesamte Netz und ändert dabei jeweils nur einen Aspekt“, erklärt Frank van Bussel vom Max-Planck-Institut für Dynamik und Selbstorganisation (MPIDS). Mit zunehmender Anzahl von Knoten nimmt die Rechenzeit deshalb dramatisch zu. Für ein quadratisches Gitter von der Größe eines Schachbretts etwa beträgt sie schätzungsweise viele Milliarden Jahre.

“Kurzsichtigkeit“ vereinfacht Rechenoperationen

Der neue Algorithmus, den die Wissenschaftler aus Göttingen entwickelt haben, ist deutlich schneller. „Unsere Rechnung für das Schachbrett-Gitter dauert nur sieben Sekunden“, führt Denny Fliegner vom MPIDS aus. Der Trick: Mit der neuen Methode hangeln sich die Forscher von Knoten zu Knoten durch das Netz. Als sei das Computerprogramm kurzsichtig, berücksichtigt es stets nur den nächsten Knotenpunkt. Das gesamte Netz hat es nicht im Blick. Am ersten Knotenpunkt etwa, kann es zwar noch keine Farbe endgültig auswählen. Denn dafür müsste es wissen, wie alle anderen Knoten miteinander verbunden sind.

Doch anstatt diese Frage sofort zu klären, notiert das Programm für den ersten Gitterpunkt eine Formel, die diese Unwägbarkeit als unbekannte Größe enthält. Beim Fortschreiten durch das Netz werden nach und nach alle Verbindungen sichtbar und die Unbekannten entfallen. Am letzten Knotenpunkt angekommen, kennt das Programm dann das gesamte Netz.

Anwendung bei komplizierten Fällen

Diese neue Methode ist auf deutlich komplizierte Fälle anwendbar als der bisherige Standard-Algorithmus. „Wir können nun viele Fragen aus Physik, Graphentheorie und Informatik beantworten, die bisher praktisch unlösbar waren“, sagt Marc Timme vom MPIDS. „Unsere Methode lässt sich beispielsweise auch auf antiferromagnetische Festkörper anwenden“, fügt er hinzu.

In diesen Festkörpern besitzt jedes Atom einen inneren Drehimpuls, den so genannten Spin, der verschiedene Werte annehmen kann. Die atomaren Spins richten sich in der Regel so aus, dass benachbarte Atome verschiedene Spins aufweisen. Die Anzahl der möglichen Anordnungen ist nun auch in der Praxis berechenbar. Daraus können Physiker auf grundlegende Eigenschaften der Thermodynamik von Festkörpern schließen.

(Max-Planck-Institut für Dynamik und Selbstorganisation, 09.02.2009 – NPO)