Wie kommt man nun von der Formel zur Vorhersage des Torergebnisses für ein WM-Spiel? Dafür benötigen wir zunächst Durchschnittswerte für die Torzahl – also die Anzahl an Toren, die am häufigsten, zweithäufigsten etc. bei einer Fußball-Partie herauskommen – egal welche Mannschaften spielen. Als Grundlage nehmen wir der Einfachheit halber Spiele der Bundesliga. An ihnen können wir nun überprüfen, ob die Torverteilung tatsächlich einer klassischen Poisson-Kurve folgt. Denn nur dann passt unsere Formel.
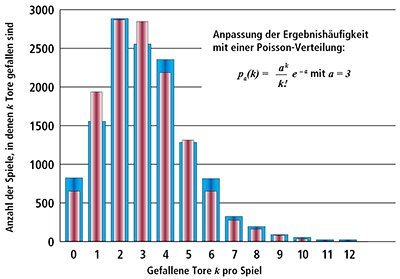
Die Grafik zeigt die Zahl der Bundesligaspiele (bis zur Saison 2005/06) und die Zahl der Treffer, die in den Spielen gefallen sind. An den blauen Säulen in der Abbildung lässt sich ablesen, dass in 2.550 Spielen 3 Tore in der Bundesliga gefallen sind. Das sind alle Spiele mit den Endergebnissen 3:0, 2:1, 1:2 und 0:3. Es gibt auch torlose Partien, nämlich die mit dem Ergebnis 0:0.
Die blaue Säule für k = 0 zeigt, dass etwa 820 Spiele ohne Torerfolg blieben. Offensichtlich gibt es am meisten Spiele mit 2 Toren, weil Endergebnisse wie 2:0, 0:2 und 1:1 relativ häufig vorkommen. Auch die blaue Säule für 4 Tore ist noch recht hoch, und 4 Tore sind damit entsprechend häufig, während die blauen Säulen für mehr als 4 Tore sehr schnell kleiner werden.
Übereinstimmung von Wirklichkeit und Modell
Dass man diese Zahlen auch theoretisch berechnen kann, zeigen die roten Säulen der Grafik. Diese wurden mit der Poisson-Formel für die mittlere Toranzahl a = 3 berechnet. Man erkennt, dass diese Formel die Verteilungskurve der Anzahl der Spiele mit jeweils k Toren recht gut wiedergibt. Natürlich ist die Übereinstimmung nicht perfekt. So gibt es offensichtlich mehr torlose Partien in der Bundesliga, als es die Poisson-Kurve prognostizieren würde. Dafür gibt es in der Theorie etwas mehr Ergebnisse mit einem Tor, also die Resultate 1:0 und 0:1, als bisher in der Realität.
Aber dennoch: Die Poisson-Kurve erklärt überraschend gut die Zahl der Spiele, die mit einer bestimmten Anzahl geschossener Tore enden. Eine Fußballmannschaft schießt also tatsächlich nach dem gleichen Zufallsschema Tore, nach dem ein radioaktiver Atomkern zerfällt – wer hätte das gedacht!
Metin Tolan, TU Dortmund / DFG Forschung
Stand: 06.06.2014






