Nach 400 Jahren endlich formell bewiesen: Wie sich Kugeln am dichtesten packen lassen, beschrieb der Astronom Johannes Kepler schon im Jahr 1611. Doch den vollständigen formellen Beweis dafür, dass seine Vermutung auch für alle denkbaren Kugelmengen und Raumgrößen gilt, lieferten Mathematiker erst 1998. Dieser Beweis war jedoch so komplex, dass menschliche Gutachter an ihre Grenze stießen. Erst jetzt haben Computerprogramme die Gültigkeit dieses Beweises bestätigt.
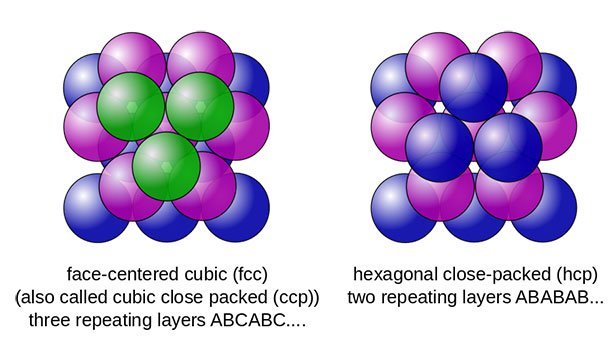
Die Keplersche Vermutung ist ein Klassiker der Geometrie: Es geht um die Frage, wie sich Kugeln am dichtesten in einem begrenzten Raum stapeln lassen – beispielsweise Orangen in einer Kiste. Intuitiv ist die Lösung einfach – und auch einfach auszuprobieren: Am wenigsten Raum nehmen die Kugeln ein, wenn sie pyramidenförmig – und damit beispielsweise kubisch-flächenzentriert oder hexagonal – gestapelt werden: Jede Kugel liegt in den Lücken der darunterliegenden Schicht.
Diese Lösung erkannte schon im Jahr 1611 der Astronom und Mathematiker Johannes Kepler. Ihm zufolge erreicht man mit dieser optimalen Stapelung eine Dichte von rund 74 Prozent. Doch das Problem war der mathematische Beweis: Dieser muss die Keplersche Vermutung für alle möglichen Raumgrößen und Kugelanordnungen mathematisch herleiten und belegen. Daran jedoch scheiterten Mathematiker Jahrhunderte lang.
Endlich ein Beweis – oder doch nicht?
1998 dann legte Thomas Hales von der University of Pittsburgh den lange gesuchten Beweis vor. Er hatte mit Hilfe eines Computerprogramms 5.000 verschiedene Kugelanordnungen durchgerechnet und für alle die Gültigkeit von Keplers Vermutung bewiesen. Das Problem dabei: Die Berechnungen dafür waren tausende Scriptzeilen lang und füllten ausgedruckt 250 Seiten.
„Das Urteil der Gutachter war damals, dass der Beweis zu funktionieren scheint, aber sie hatten nicht die Zeit oder Energie, um alles zu verifizieren“, berichtet Henry Cohn, Herausgeber der Fachzeitschrift „Forum of Mathemathics Pi“. Der Beweis von Hales wurde daher im Jahr 2005 veröffentlicht, aber die letzte Sicherheit zu seiner Gültigkeit fehlte. „Das war eine unbefriedigende Situation“, so Cohn.
Computerprogramme als Prüfer
Um dieses Problem zu lösen, kamen Hales und seine Kollegen auf die Idee, Computer als Prüfer zu nutzen. Zwei spezielle Proof-Checker-Programme, HOL Light und Isabelle, die normalerweise unter anderem zur Fehlersuche in Software eingesetzt werden, testeten dabei Hales Beweis auf logische Konsistenz. „Das Flyspeck-Projekt dürfte den Rekord in Bezug auf die überprüften Codezeilen in einem Verifikationsprojekt halten“, sagt Hales.
Wie die Forscher erklären, dauert die Prüfung des Hauptteils von Hales Beweis nur rund einen Tag. Doch für eine der drei Unterklassen benötigen die Programme 5.000 CPU-Stunden. Diese Prüfungen haben die Forscher mehrmals hintereinander wiederholt. Jetzt sind sie abgeschlossen und Hales und seine Kollegen haben das Ergebnis veröffentlicht.
Es bestätigt: Hales formaler Beweis von Keplers Vermutung ist gültig. Nach gut 400 Jahren ist damit das Kugelstapel-Problem auch mathematisch formal und vollständig gelöst, wie die Mathematiker erklären. (Forum of Mathematics Pi, 2017; doi: 10.1017/fmp.2017.1)
(Cambridge University Press, 19.06.2017 – NPO)














