Dass die Intervalle bestimmte Stimmungen symbolisieren, ist den Musikern bekannt und wird von ihnen daher bewusst eingesetzt, um bestimmte Stimmungen zu erzeugen. Dass der Mensch auf bestimmte Intervalle aber auch mit entsprechenden Erregungsmustern im Gehirn reagiert, hat erst eine Studie gezeigt. Sie wurde im Rahmen eines Projekts durchgeführt, das nichts Geringeres will, als das Gesetz hinter dem Wohlklang auch mathematisch zu beweisen.
Ein Gesetz für alle
Guerino Mazzola, Mathematiker und Jazzpianist, arbeitet seit Jahren daran, das subjektive Erleben konsonanter und dissonanter Klänge objektiv erklärbar zu machen. Bereits Arnold Schönberg, der Begründer der Zwölftonmusik, die das traditionelle Tonsystem aus Dur und Moll auflöst und eine Gleichberechtigung aller Töne, die „Emanzipation der Dissonanz“ einführte, war der Meinung, dass die verschiedenen Tonsysteme auf allgemeinen Gesetzmäßigkeiten beruhen mussten.
Um diesen Gesetzmäßigkeiten auf die Spur zu kommen, nahm sich Mazzola zunächst des Grundbausatzes der abendländischen Musik an, der zwölf Töne einer Oktave. Die Töne teilte er in zwei Gruppen zu je sechs. Rechnerisch gibt es immerhin 924 Möglichkeiten einer solchen Einteilung. Mazzola stellte jedoch fest, dass sechs dieser Aufteilungsweisen durch besondere Symmetrien mathematisch auffällig sind. Er nannte diese sechs Gruppen „starke Dichotomien“.
Der Terzen-Tonus
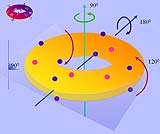
Die zwölf Töne sind bei Mazzola von 0 bis 11 nummeriert, die sich daraus ergebenden Intervalle untersuchte er in einem speziellen Koordinatensystem – dem „Terzen-Torus“. Das musikalische Intervall der Terz kann in der Praxis aus drei oder aus vier Halbtonschritten bestehen, die kleine und die große Terz. Innerhalb des Terzen-Torus wurden die zwölf Töne nun so angeordnet, dass die jeweils benachbarten Punkte zueinander im Abstand einer Terz stehen – und zwar einer kleinen Terz in eine Richtung und einer großen Terz in die andere.
Drei große oder vier kleine Terzen sind in der Summe wieder eine Oktave. So schließt sich das Diagramm Mazzolas zu einer Art „Schwimmreifen“, dem bereits erwähnten Terzen-Torus. Die Abstände der Töne auf diesem Diagramm lassen sich berechnen. Mazzola definierte zwei Größen, nach denen er die Dichotomien, die in zwei Gruppen sortierten Töne, beurteilte. Der „Durchmesser“ ist bei Mazzola die Summe aller Abstände, den die Töne einer Sechsergruppe zueinander haben. Die „Spannweite“ ist die Summe der Abstände aller sechs Töne zu den Tönen, mit denen sie durch bestimmte Symmetrien verbunden sind.
Die Mathematik der Schönheit
Innerhalb der sechs „starken Dichotomien“ gibt es eine Extrem-Variante, die den maximalen Wert aller Spannweiten und den minimalen Wert aller Durchmesser erreicht. Unter den 924 Möglichkeiten hat diese die Nummer 82. Überraschend: In der einen Gruppe bilden die sechs Töne ausschließlich konsonante Intervalle der abendländischen Musik, in der anderen nur dissonante. Die Beziehung der Konsonanten und Dissonanten konnte Mazzola in einer einfachen mathematischen Formel darstellen.
Doch die größte Überraschung des Modells: Es wurde durch eine Studie bestätigt, die die Gehirnströme von Probanden untersuchte, während diese die zwölf musikalischen Intervalle zu hören bekamen. Dabei entstanden zwei verschiedene Erregungsmuster im Hippocampus, die genau den Intervall-Sechsergruppen in Dichotomie Nummer 82 entsprechen.
Auch die Dichotomie Nummer 64 mit den entgegengesetzten Eigenschaften von Nummer 82 – maximaler Durchmesser und minimale Spannweite – fiel besonders auf. Die eine der beiden Intervall-Gruppen vereinte sechs der Töne, die zu den Grundtönen einer C-Dur-Tonleiter gehören, der wir als reinste aller Tonleitern empfinden.
Offenbar scheint das vermeintlich subjektive Gefühl für schöne Musik exakt mit der besten mathematischen Lösung übereinzustimmen, Entweder ist dies Zufall oder das Ergebnis einer Auslese, die während der Jahrhunderte langen Musikgeschichte bestimmte Frequenzen zu den „schönsten“ gemacht hat.
Stand: 02.03.2007