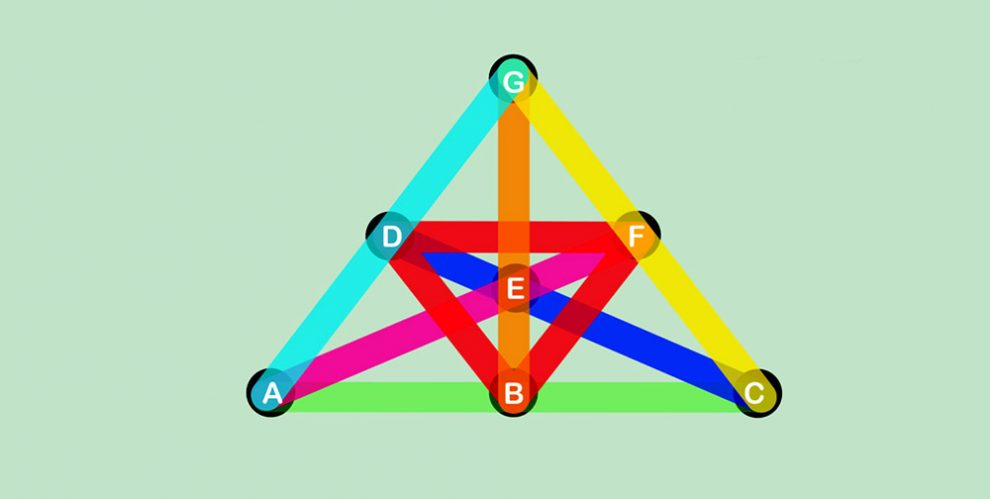
Nach 50 Jahren gelöst: Mathematiker haben eine der berühmten Erdös-Vermutungen bewiesen – die Existenz sogenannter Steiner-Tripelsysteme mit hoher Taillenweite. Sie besagt, dass beispielsweise sieben Personen sieben Trios bilden können, ohne dass sich dasselbe Paar in mehr als einem Tripel findet. Indem die Forscher Methoden aus der Wahrscheinlichkeitstheorie anwendeten, gelang es ihnen, diese Vermutung erstmals zu beweisen.
Der ungarische Mathematiker Paul Erdös gilt als einer der bedeutendsten Mathematiker des 20. Jahrhunderts. Er stellte zahlreiche Sätze und Vermutungen in der Zahlentheorie und Kombinatorik auf, darunter einige, die sich mit der geometrischen Ordnung von Graphen beschäftigen. Einige dieser kombinatorischen Designs sind nicht nur für abstrakte Zusammenhänge relevant, sondern auch ganz praktisch für die Entwicklung von Experimenten und Computercodes.
Trios ohne doppelte Paare gesucht
Eine dieser Erdös-Vermutungen beschäftigt sich mit sogenannten Steinerschen Tripelsystemen – der Anzahl möglicher Dreier-Kombinationen unter bestimmten Einschränkungen. Ein Beispiel: Angenommen, sieben Personen wollen Dreiergruppen bilden. Jede Person kann Teil mehrerer Tripel sein, aber jedes Personenpaar darf nur Teil von exakt einer Dreiergruppe sein. Wird diese Bedingung mit einer hohen Zahl von Tripeln und wenigen Personen erfüllt, spricht man von einer hohen Taillenweite.
Erös postulierte, dass solche Tripelsystem möglich sind, doch ein Beweis für Tripelsysteme mit mehr als sechs Personen stand bisher aus. “ Probleme dieses Typs sind im Allgemeinen ungeheuer schwierig zu beweisen und es erschient fast weit außerhalb unserer Reichweite, die Zahl der Tripel präzise zu charakterisieren, die es für eine vorgegebene Konfiguration gibt“, erklären Matthew Kwan vom Institute of Science and Technology Austria (ISTA) und seine Kollegen.
Kombination mathematischer Methoden
Doch genau dies ist dem Mathematiker-Team nun gelungen. Kwan und seine Kollegen haben in ihrer Arbeit die Existenz von Steiner-Tripelsystemen mit beliebig hoher Taillenweite bewiesen. „Um ihre Existenz zu beweisen, muss man die Algebra vermeiden und Methoden aus der Wahrscheinlichkeitstheorie, der Probabilistik, einführen“, erklärt Kwan. „Das ist uns gelungen.“
Dafür nutzten sie eine Breite Palette an mathematischen Verfahren, die vor allem auf der probabilistischer Kombinatorik basiert. „Zusätzlich haben wir zwei neue Methoden benutzt: Die Retrospektive Analyse, die es uns ermöglicht, die Zufälligkeit in früheren Schritten nachzuverfolgen, und die Sparsification, eine Art Ausdünnung, die alle Herausforderungen der retrospektiven Analyse beseitigt“, erklärt Kwan.
Vermutung bewiesen
Dadurch gelang es dem Team, die vor 50 Jahren aufgestellte Erdös-Vermutung zu knacken. „Wir können unter anderem beweisen, wo die Untergrenze für die Zahl der r-sparsamen Steiner-Tripelsysteme bei einem gegebenen Satz von Eckpunkten liegt“, erklären sie. Dadurch zeigten die Mathematiker unter anderem, dass bei sieben Eckpunkten genau sieben Tripel ohne doppelte Paarungen möglich sind.
Wie Kwan erklärt, gelang dieser Durchbruch erst durch die übergreifende Anwendung von Techniken aus verschiedenen Teilgebieten der Mathematik. „Meine Philosophie: Ich versuche, an verschiedenen Dingen zu arbeiten“, so der Mathematiker. „Es mag verlockend sein, sich komplett auf ein Teilgebiet zu konzentrieren, aber wenn man sein ganzes Leben lang an verschiedenen Problemen tüftelt, findet man jene Techniken, die einem helfen, in anderen Bereichen Neues zu entdecken.“ (Preprint arXiv: 2201.04554v3)
Quelle: Institute of Science and Technology Austria