Angriff auf die Kryptografie: Eine neue Quanten-Architektur könnte gängige Verschlüsselungen auf Basis multiplizierter Primzahlen knacken helfen. Denn das Quantensystem kann normalerweise unumkehrbare logische Operationen reversibel machen – und so selbst große Zahlen in ihre Primzahlfaktoren zerlegen. Allerdings: Um das zurzeit gängige 2048-Bit-Protokoll der RSA-Verschlüsselung zu knacken, bräuchte man selbst mit diesem System rund 14 Millionen Quantenbits.
Gängige Kryptografie-Methoden nutzen durch Multiplikation von Primzahlen erzeugte Zahlen, um Daten zu verschlüsseln. Denn die resultierenden Zahlen wieder in ihre Primzahlfaktoren zu zerlegen, ist wegen der unzähligen Möglichkeiten enorm rechenaufwändig und für klassische Computer kaum zu schaffen. Anders ist dies jedoch bei Quantencomputern: Weil ein Quantencomputer durch die Überlagerung von Zuständen stärker parallel rechnet als klassische Computer, kann er solche Aufgaben deutlich schneller bewältigen.
Schon 1994 hatte der USA-Mathematiker und Informatiker Peter Shor einen Algorithmus für Quantencomputer entwickelt, der eine solche Faktorisierung erlauben würde. Seither wurde der Shor-Algorithmus schon auf ersten Quantencomputern getestet und weiter optimiert. Diese Ansätze beruhen allerdings noch immer auf der klassischen Brute-Force-Methode, bei der durch Ausprobieren aller Möglichkeiten nach der richtigen Primzahlzerlegung gesucht wird – und sind entsprechend ineffizient.
Das Problem der Unumkehrbarkeit
Doch es geht auch anders, wie nun Martin Lanthaler von der Universität Innsbruck und seine Kollegen demonstrieren. Sie haben den Bauplan für eine neue, effizientere Faktorisierung mithilfe von Quantencomputern entwickelt. Ihre Methode setzt an genau der Eigenschaft an, die die Primzahlmultiplikation so attraktiv für heutige Verschlüsselungen macht: Sie ist nicht umkehrbar – man kann die Multiplikation nicht einfach wieder rückgängig machen.
„Nimmt man die Multiplikation 2*2=4, so kann man diese Operation nicht einfach umgekehrt ablaufen lassen, denn 4 könnte 2*2 sein, aber genauso 1*4 oder 4*1“, erklärt Seniorautor Wolfgang Lechner von der Universität Innsbruck. Auch die logischen Gatter, mit denen klassische Computer diese Operationen durchführen, sind irreversibel: Die Algorithmen können nicht rückwärts ablaufen. „Diese inhärente Asymmetrie von Multiplikation und Faktorisierung bildet die Basis für Kryptografie-Protokolle wie RSA“, so das Team.
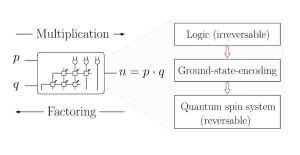
Spinzustände ermöglichen Umkehrung der Operation
Jetzt haben Lanthaler und seine Kollegen jedoch eine Quantenarchitektur entwickelt, die genau diese Umkehrung erlaubt und damit die Asymmetrie von Multiplikation und Faktorisierung aufhebt. Möglich wird dies, weil die Physiker die logischen Schaltkreise in den Grundzuständen von Quantenbit-Spins kodieren. Die für die Multiplikation und Zerlegung nötigen Operationen werden dabei als UND-Gatter, Halb- und Volladdierer über Spinzustände der Qubits realisiert.
Der Clou daran: Während die logischen Gatter irreversibel sind, gilt dies für die wechselwirkenden Spinzustände von Quantenteilchen nicht: „Damit kann sowohl Multiplikation als auch Faktorisierung als Grundzustandsproblem verstanden und mit Methoden der Quantenoptimierung gelöst werden“, erklärt Lechner. Denn um den Grundzustand zu finden und damit das Optimierungsproblem zu lösen, muss nicht die ganze Energielandschaft abgesucht werden, sondern tieferliegende Täler können durch „Tunneln” erreicht werden.
Effizienter und schneller als Brute-Force
Anstelle der klassischen Brute-Force-Methode erlaubt die neue Quantenarchitektur es damit, den Suchprozess nach den richtigen Primzahlfaktoren deutlich zu beschleunigen. „Unser problemspezifischer Ansatz reduzierte zudem den Hardware-Aufwand, dadurch benötigen wir beispielsweise weniger Qubits als Brute-Force-Ansätze“, erklären Lanthaler und seine Kollegen. Das könnte künftige Codeknacker-Quantencomputer effizienter machen.
Positiv auch: Das gesamte Faktorisierungs-Schema kann auf einer Vielzahl von Qubit-Plattformen umgesetzt werden – von supraleitenden Transmon-Qubits über Ionen-Qubits bis zu neutralen Rydberg-Atomen als Recheneinheiten, wie die Physiker erklären. Die Codierung erlaubt es zudem, den ganzen Schaltkreis aus sich wiederholenden Subsystemen aufzubauen und so die Leistung zu skalieren.
Nötige Qubit-Zahl noch nicht erreicht
Allerdings: Bisher benötigt auch diese neue Quantenlösung für das Faktorisierungsproblem große Mengen an Quantenbits: „Das gängige RSA2048-Protokoll nutzt einen Schlüssel mit 2048 Bits. Um ihn mit unserem Ansatz zu knacken, bräuchte man rund 14 Millionen Qubits“, erklären die Physiker. Die größten aktuellen Quantencomputer umfassen nur etwas mehr als 100 Qubits. Bis diese Rechner zur Gefahr für die RSA-Verschlüsselung werden, bleibt daher noch etwas Zeit. (Communications Physics, 2023; doi: 10.1038/s42005-023-01191-3)
Quelle: Universität Innsbruck