42 Ziffern, 32 Jahre der Suche: Mathematiker haben die sogenannte neunte Dedekind-Zahl ermittelt – eine 42-stellige Zahl, die die Lösung einer Zahlenfolge auf Basis monotoner boolescher Funktionen repräsentiert. Bisher waren nur die ersten acht Werte für diese Folge bekannt, weil es schlicht an Rechenleistung fehlte, um sie auch für n=9 zu lösen. Doch jetzt ist dies gelungen: Dank besonders effizienter Lösungsalgorithmen und großer Supercomputer ermittelten Mathematiker für die neunte Dedekind-Zahl den Wert von 286386577668298411128469151667598498812366.
Ob die Erdös-Vermutung, die Diophantische Gleichung oder die scheinbar triviale Frage, wie sich Kugeln am dichtesten packen lassen: Viele mathematische Fragen werden erst nach Jahrzehnten oder sogar Jahrhunderten geknackt. Andere sind dagegen noch immer ungelöst, wie etwa das berühmte p=np-Problem oder die Frage, ob es wirklich unendlich viele Primzahlzwillinge gibt. Dazu kommen mathematische Zahlenfolgen und Funktionen, deren Berechnung so aufwendig ist, dass bisher erst wenige Werte dafür ermittelt werden konnten.
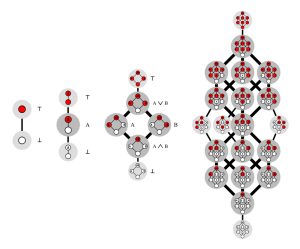
Multidimensionale Würfel und farbige Schnitte
Zu diesen schwer berechenbaren Funktionen gehören auch die sogenannten Dedekind-Zahlen. Diese 1897 vom deutschen Mathematiker Richard Dedekind definierte Folge ganzer Zahlen gibt an, wie viele monotone boolesche Funktionen es in n-Variablen gibt. „Grundsätzlich kann man sich eine monotone boolesche Funktion in zwei, drei und unendlich vielen Dimensionen als ein Spiel mit einem Würfel vorstellen“, erklärt Lennart Van Hirtum von der Universität Paderborn.
„Man balanciert den Würfel auf einer Ecke und färbt dann jede der übrigen Ecken entweder weiß oder rot. Dabei gibt es nur eine Regel: Man darf niemals eine weiße Ecke oberhalb einer roten platzieren“, so der Mathematiker weiter. „Dadurch entsteht eine Art vertikaler Rot-Weiß-Schnitt. Das Ziel des Spiels ist es, zu zählen, wie viele verschiedene Schnitte es gibt.“ Die Anzahl dieser Schnitte ergibt die Dedekind-Zahl M(n).
Gigantische Zahlenwerte
Das Problem jedoch: Je mehr Dimensionen der gedachte Würfel hat, desto komplizierter wird es, den Dedekind-Wert zu ermitteln. „Auch wenn es nicht so wirkt, die Zahlen werden dabei schnell gigantisch: Die achte Dedekind-Zahl hat bereits 23 Ziffern“, erläutert Van Hirtum. Hinzu kommt, dass es eine effiziente, geschlossene Formel für die Berechnung der Dedekind-Zahl bisher nicht gibt. Um die Zahl zu berechnen, nutzte man bisher meist Summationsformeln. Diese jedoch werden mit steigendem Wert für n schnell extrem umfangreich und aufwendig.
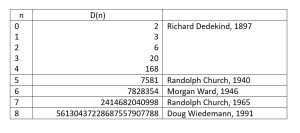
„32 Jahre lang war die Berechnung von D(9) eine offene Herausforderung und es war fraglich, ob es überhaupt möglich ist, diese Zahl jemals zu errechnen“, sagt Van Hirtum. Schon für die achte, im Jahr 1991 geknackte Dedekind-Zahl benötigte man einen Cray-2-Supercomputer, einen der damals leistungsfähigsten Rechner weltweit. Seither hat die Computertechnik jedoch Fortschritte gemacht und auch mathematisch gibt es neue Lösungsansätze. „Uns schien es deshalb denkbar, dass es inzwischen möglich sein sollte, die neunte Zahl auf einem großen Supercomputer zu berechnen“, so Van Hirtum.
Fast so viele Terme wie Sandkörner auf der Erde
Van Hirtum und sein Team nutzten für die Lösung von D(9) eine Technik, die als P-Koeffizienten-Formel bekannt ist. Sie bietet eine Möglichkeit, Dedekind-Zahlen nicht durch Zählen, sondern durch eine sehr große Summe zu berechnen. Allerdings wächst die Anzahl der Terme in dieser Formel so schnell an, dass die Mathematiker eine Optimierung und „Verschlankung“ der Methode finden mussten.
„In unserem Fall konnten wir durch Ausnutzung von Symmetrien in der Formel die Anzahl der Terme auf ‚nur‘ 5,5 mal 1018 reduzieren – eine enorme Menge. Zum Vergleich: Diese Menge kommt der Zahl der Sandkörner auf der gesamten Erde sehr nahe. Dennoch ist eine solche Anzahl von Rechenoperationen für einen modernen Supercomputer prinzipiell kein Problem – er benötigt dafür aber sehr viel Zeit. Selbst mit Grafikprozessoren als aktuell schnellster Hardwarebeschleuniger-Technologie würde die Berechnung der neunten Dedekind-Zahl mit diesem Algorithmus zu lange dauern.
Supercomputer mit spezieller Hardware-Beschleunigung
Als zweiten Teil der Lösung musste das Team daher eine anwendungsspezifische Hardware entwickeln, die für die nötigen Rechnungen optimiert ist. Van Hirtum entwickelte dafür einen Hardware-Beschleuniger auf Basis sogenannter FPGAs (Field Programmable Gate Arrays), einer Form hochspezialisierter und paralleler Rechenwerke. Um diesen einzusetzen, benötigte er jedoch einen Supercomputer, der über entsprechende FPGA-Karten verfügt.
Diesen fand der Mathematiker mit dem Supercomputer Noctua-2 im „Paderborn Center for Parallel Computing (PC2)“. „Noctua 2 ist einer der wenigen Supercomputer weltweit, mit denen das Experiment überhaupt durchführbar ist“, erklärt Koautor Christian Plessl von der Universität Paderborn. „Die extremen Anforderungen an Zuverlässigkeit und Stabilität stellen auch eine Herausforderung und Test für unsere Infrastruktur dar.“ Doch durch mehrere Jahre dauernde Anpassungen und Optimierungen gelang es.
D(9) ist gefunden!
Van Hirtum und seine Kollegen ließen das Programm fünf Monate lang auf dem Supercomputer Noctua 2 laufen. Dann lieferte es die Lösung: Am 8. März 2023 hatten die Wissenschaftler die 9. Dedekind-Zahl gefunden. Sie hat 42 Stellen und lautet 286386577668298411128469151667598498812366. 32 Jahre nach der achten Dedekind-Zahl ist die Zahlenfolge damit um einen weiteren Eintrag gewachsen.
Nur knapp einen Monat später, Anfang April 2023, veröffentlichte ein zweiter Mathematiker seine Lösung für die neunte Dedekind-Zahl – unabhängig von Van Hirtum und seinem Team war Christian Jäckel von der Technischen Universität Dresden auf den gleichen Wert gekommen. Auch er hatte Symmetrien in den Formeln und optimierte Algorithmen für die Berechnung dieser Zahl genutzt. (arXiv:2304.03039; arXiv:2304.00895)
Quelle: Universität Paderborn