Auf eine weitere Merkwürdigkeit der Primzahlen stieß vor gut 200 Jahren ein 15-jähriges Mathe-Wunderkind: Carl Friedrich Gauß. Wie viele seiner mathematisch interessierten Zeitgenossen beschäftigte sich auch Gauß damit, Primzahlen im Zahlenraum aufzuspüren. Dafür teilte er die Zahlen in Tausendergruppen ein, identifizierte darin die Primzahlen und zählte ihre Anzahl.
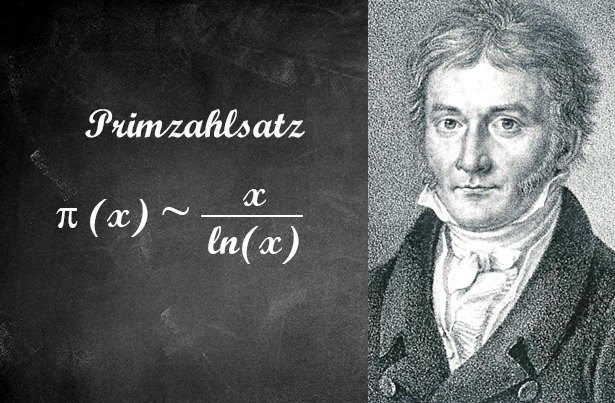
Primzahldichte und der natürliche Logarithmus
Dabei stellte Gauß Überraschendes fest: Je größer die Zahlenräume werden, desto weniger Primzahlen enthalten sie. Anders ausgedrückt: Die Dichte der Primzahlen verringert sich, je mehr Stellen die Zahlen haben. Dabei scheint ihre Häufigkeit sogar einer Gesetzmäßigkeit zu folgen – und in ihr die spielt der natürliche Logarithmus eine entscheidende Rolle. Mit seiner Hilfe lässt sich abschätzen, wie viele Primzahlen sich im Zahlenraum bis zu einer bestimmten Zahl verbergen.
Gauß‘ Vermutung bildet heute den Primzahlsatz – ein weiteres fundamentales Theorem der Mathematik. Nach diesem kann man die Anzahl der Primzahlen im Zahlenraum bis zu einer Zahl x mthilfe einer Funktion des natürlichen Logarithmus von x abschätzen. Entspricht x beispielsweise einer Milliarde, dann ist der natürliche Logarithmus davon rund 21. Der Anteil der Primzahlen im Zahlenraum bis einer Milliarde liegt demnach bei rund 1/21 – das entspricht rund fünf Prozent. Rechnet man dies für größere Zahlenwerte durch, sinkt der Anteil der Primzahlen.
Das Rätsel der Lücken
Doch aus dem Primzahlsatz ergibt sich noch etwas: Mit ihm kann man ermitteln, wie groß im Durchschnitt der Abstand zwischen zwei aufeinanderfolgenden Primzahlen sein muss. Die Größe der Lücke entspricht demnach im Schnitt dem natürlichen Logarithmus der Zahl n. Ist n= eine Milliarde wie in unserem Beispiel, dann ist die Lücke zwischen zwei Primzahlen in diesem Bereich im Mittel 21 Zahlen lang. Der Primzahlsatz liefert damit eine grobe Faustregel für den durchschnittlichen Abstand.
Doch wie groß kann der Abstand zwischen zwei Primzahlen maximal werden? „Das ist eine eigentlich offensichtliche Frage, für manche vielleicht eine der ersten, die ihnen zu Primzahlen einfallen“, sagte Andrew Granville von der University of Montreal im Magazin Quanta. „Doch bei der Suche nach der Antwort stecken wir seit knapp 80 Jahren fest.“ Klar ist: Immer wieder gibt es ungewöhnlich große Lücken zwischen aufeinanderfolgenden Primzahlen. Das Problem liegt jedoch darin, diese Lücken aufzuspüren und die Formeln, die ihre maximale Größe beschreiben, auch zu beweisen.
Die magischen 70 Millionen
Die Beschäftigung mit großen Primzahlenlücken dabei mehr als ein bloßes Zahlenspiel. Sie kann auch eine ganz praktische Konsequenz haben: Vielstellige Primzahlen bilden die Basis vieler gängiger Verschlüsselungsverfahren. Sie werden dafür von speziellen Algorithmen erzeugt, sogenannten Primzahlengeneratoren. „Doch wenn sie Pech haben und am Anfang einer dieser riesigen Lücken ihre Suche beginnen, dann könnte der Algorithmus sehr lange brauchen, um fündig zu werden“, erklärt der Mathematiker James Maynard von der University of Oxford.
Im Jahr 2013 löste der zuvor weitgehend unbekannte Mathematiker Yitang Zhang von der University of New Hampshire eine Sensation unter den „Lückenfahndern“ aus: Er bewies erstmals, dass sich der Abstand zwischen zwei Primzahlen eingrenzen lässt. Seinen Berechnungen nach gibt es im unendlichen Zahlenstrang unendlich viele Primzahl-Nachbarn, die durch nicht mehr als 70 Millionen Zwischenzahlen getrennt sind. „Das ist ein fantastischer Durchbruch, ein historisches Ergebnis“, kommentiert Granville.
Nadja Podbregar
Stand: 15.06.2018








