In der chemischen Analytik, in der Wetter- und Erdbebenvorhersage, sogar in den Rechts- und Wirtschaftswissenschaften waren neuronale Netze lange Zeit in Mode: Mit ihrer Hilfe kann man riesige Datenmengen nach verborgenen Zusammenhängen durchforsten, die der puristischen, klassischen Analyse verborgen geblieben wären. Heute ist ihr Stern jedoch ein wenig im Sinken begriffen. Präzisere, aber in der dahinter stehenden Theorie ungleich anspruchsvollere Analysemethoden und die Leistungsfähigkeit schneller Rechner haben den Softwareneuronen den Rang abgelaufen.
Denn der Segen der neuronalen Netze ist zugleich ihr Fluch: Mit ihnen lässt sich zwar prinzipiell der Verlauf jeder beliebigen mathematischen Funktion annähern. Leider verrichten sie ihren Job in der Praxis aber nur mit mäßiger Genauigkeit. Um dies zu verstehen, reicht ein Blick auf ihre Funktionsweise. So geht ihr Arbeitsprinzip auf eine Idee des russischen Mathematikers Andreij Nikolajewitsch Kolmogorow zurück, eines der bedeutendsten mathematischen Köpfe des 20. Jahrhunderts.
Kolmogorow machte sich im Jahr 1948 noch recht abstrakte Gedanken über ein „Black-Box-System“, das jeden wie auch immer gearteten Input auf logische Weise mit einem passenden Output verbinden kann – wie eine Parabelfunktion ein x mit einem y verbindet. Nur eben viel universeller. Am einfachsten lässt sich der „universale Approximator neuronales Netz“ tatsächlich durch einen Vergleich mit echten Nervenzellen verstehen.
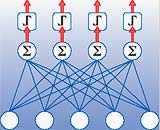
Bekanntlich besteht das Gehirn aus einer Vielzahl einander sehr ähnlicher Zellen (Neuronen), die über gewisse Leitungen mit anderen, gleichartigen verschaltet sind, die wiederum Kontakt zu weiteren haben. In der Natur kann eine einzelne Nervenzelle mit tausenden anderer verbunden sein. Wenn ein solches Neuron dann von seinen Nachbarn mit Signalen bestürmt wird, macht es zunächst nichts weiter, als diese eingehenden Signale zu summieren. Erreicht die Summe aller Anrufe zusammengenommen einen gewissen Schwellenwert, entscheidet sich das Neuron, seinerseits ein Signal zu feuern, das nun zur Erregung der Nachbarzellen beiträgt.
Oder eben nicht. Denn ein klein wenig komplexer ist die Geschichte schon: So gibt es zum Beispiel nicht nur erregende, sondern auch dämpfende Signale. Und: Nervenzellen sind in der Lage, jeder Leitung eine gewisse Bedeutung oder Wichtigkeit beizumessen. So können wenige Signale, die über starke Leitungen ankommen – man denke an die roten Telefone im Kanzleramt – genügen, um die Zelle zum Feuern zu veranlassen, während tausend eingehende Signale, die über schwache Leitungen auflaufen, die Zelle noch lange nicht aus ihrer Lethargie wecken.
Gehen immer wieder sinnvolle Signale über bislang schwache Leitungen ein, können diese jedoch an Bedeutung gewinnen – so baut das Gehirn allmählich Muster aus starken und schwachen Bahnen auf, die durch immer geringere Anlässe angeregt werden können: Es lernt. Mehr braucht es im Prinzip auch im Computer nicht, um überaus komplexe mathematische Funktionen in den Griff zu bekommen.
Stand: 27.05.2005
