Eine Sache der Wahrscheinlichkeiten

Vorlesen

Die Fußball-WM in Brasilien steht vor der Tür. Schon jetzt diskutieren Fans allerorten die Frage, welches Team wohl Weltmeister werden wird. Der Gastgeber Brasilien? England? Die Niederlande? Oder doch Deutschland? Aber auch Wissenschaftler beschäftigen sich mit dieser Frage: erst vor kurzem brachten Forscher der FU Berlin ihren WM-Simulator an den Start. Er nutzt Parameter wie das offizielle FIFA-Ranking und andere Indikatoren für die Spielstärke, um den Sieger virtuell auszuspielen.

Die Wahrscheinlichkeit eines bestimmten Torergebnisses lässt sich mathematisch beschreiben. © freeimages

Der Physiker Metin Tolan, Experte für die mathematisch-physikalische Sicht auf das Spiel um den Ball, hat ebenfalls eine Simulation entwickelt. Bei dieser stehen die Tore oder vielmehr die Wahrscheinlichkeit für ein Spielergebnis im Vordergrund. Die Grundfrage dahinter: Wie wahrscheinlich ist es, dass Jogis Jungs nach 24 Jahren den heiß ersehnten Titel mit nach Hause bringen werden? Überlassen wir nun Tolan das Wort:

Spielstände als Poisson-Verteilung

Hierzu machen wir die Annahme, dass eine Fußballmannschaft im Prinzip nichts anderes ist als eine „radioaktive Quelle“, nur dass sie eben keine Strahlung emittiert, sondern Tore. Diese Annahme klingt zwar zunächst recht merkwürdig, ist aber völlig gerechtfertigt, weil die Verteilung der Anzahl der Spiele, bei denen eine gewisse Anzahl von k Toren geschossen wird, durch eine sogenannte Poisson-Verteilung gegeben ist. Diese bestimmt beispielsweise auch den radioaktiven Zerfall.

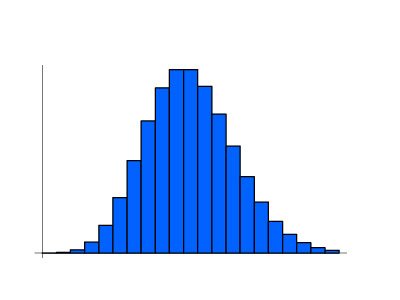
Eine Poisson-Verteilung gibt an, wie häufig ein bestimmter Wert - beispielsweise ein Torergebnis - eintritt. © gemeinfrei

Immer beginnt eine solche Verteilung bei einem festgelegten Wert, läuft dann durch ein Maximum und fällt für große Werte stark ab. Im Falle des Fußballs liegt das Maximum ungefähr bei der mittleren Anzahl a der Tore. In der Fußball-Bundesliga fallen im Durchschnitt circa 3 Tore pro Spiel, also ist in diesem Fall a = 3. Für die Poisson-Verteilung gilt dann: p_a(k) = ak• e^–a / k!

Diese Formel gibt nun an, wie groß die Wahrscheinlichkeit pa(k) ist, dass ein Spiel mit einer Gesamtzahl von k Toren endet, wenn im Durchschnitt a Tore pro Spiel fallen. Sie wurde für verschiedene Profi-Ligen und auch Nationalmannschaften in der Vergangenheit schon häufig empirisch überprüft. Die Poisson-Formel für die Torverteilung gilt auch für eine einzelne Mannschaft: Sie gibt dann die Wahrscheinlichkeit dafür an, dass eine Mannschaft in einem bestimmten Spiel k Tore erzielt, wenn sie im Durchschnitt a Tore pro Spiel schießt. Dabei ist e = 2,7182818… die sogenannte Euler’sche Zahl und k! (sprich k Fakultät) ist eine Kurzschreibweise: k! = 1•2•…•(k-1)•k.