Was in den natürlich ablaufenden, irreversiblen Prozessen geschieht, wird mit einer besonderen Größe, der Entropie, beschrieben. Hierfür gibt es zwei verschiedene Zugänge. Zum einen kann man die einzelnen Bestandteile eines Systems betrachten. Dann ist die Entropie ein Maß für die Zahl der Realisierungsmöglichkeiten eines bestimmten Zustandes.
Teilchen auf Wanderschaft
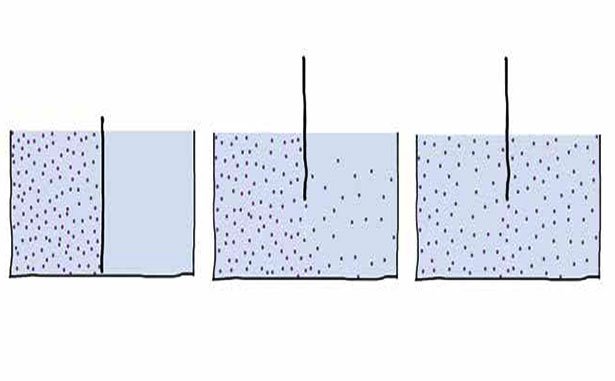
Als Beispiel soll hier ein Gefäß dienen, das durch eine herausnehmbare Wand unterteilt ist. Auf beiden Seiten der Trennwand befindet sich Wasser, aber nur auf einer der beiden Seiten ist das Wasser mit Farbe verrührt. Wird die Trennwand herausgezogen, so mischen sich die beiden Wassermengen, und die Farbe befindet sich nach einiger Zeit in gleichem Ausmaß in beiden Hälften.
Für jedes Farbstoffteilchen ist dann die Wahrscheinlichkeit, in der linken oder rechten Hälfte zu sein, gleich groß. Es wird sich jedoch praktisch nie mehr der Zustand einstellen, dass alle Farbteilchen in nur einer Hälfte versammelt sind. Der Grund ist, dass es sehr viele Realisierungsmöglichkeiten dafür gibt, dass links und rechts gleich viele Farbteilchen sind, aber nur genau eine, bei der alle Teilchen wie zu Beginn auf der linken sind.
Wenn ein System von einem Zustand mit wenigen Realisierungsmöglichkeiten und damit geringer Wahrscheinlichkeit in einen mit vielen Möglichkeiten und damit größerer Wahrscheinlichkeit übergeht, dann wächst die Entropie.












