Zurück zu den Anfängen. Zwei Jahre später, im Jahr 1978, veröffentlichten Ron Rivest, Adi Shamir
und Len Adleman vom Massachusetts Institute of Technology (MIT) den nach ihnen benannten RSA-Algorithmus, den ersten Algorithmus mittels Public Key (PK). Damit war PK-Kryptografie Realität geworden.
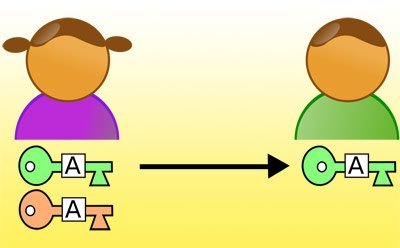
Prinzipiell besteht ein Public-Key-Verschlüsselungsverfahren aus drei Algorithmen: Der erste erzeugt ein Schlüsselpaar, das aus einem öffentlichen und dem dazugehörigen geheimen Schlüssel besteht. Der zweite verschlüsselt den Klartext unter Verwendung des öffentlichen Schlüssels. Der dritte schließlich entschlüsselt den Text wieder unter Verwendung des geheimen Schlüssels.
Das Geheimnis der modularen Exponentialfunktion
Das mathematische Verfahren, auf dem der RSA-Algorithmus und fast alle anderen Public-Key-Algorithmen beruhen, ist die „modulare Exponentiation“. Diese Exponentialfunktion, also die Funktion f(x) = gx für eine beliebige Basis (g) gehört zu den am besten untersuchten und verstandenen Funktionen der Mathematik. Im Falle des RSA-Algorithmus benutzt man dafür aber nur die natürlichen Zahlen unterhalb einer festen Zahl n, also die Zahlen 0, 1, 2, …, n-1.
Auch mit diesen Zahlen kann man rechnen, das heißt addieren, subtrahieren und multiplizieren, und zwar, indem man zunächst so rechnet wie in den natürlichen Zahlen und dann das Ergebnis durch n teilt und nur den Rest betrachtet. Im Fall n = 10 würde man also 3 x 8 ausrechnen, indem man zunächst 3 x 8 = 24 rechnet und dann als Ergebnis den Rest nimmt, der entsteht, wenn man 24 durch 10 teilt. Das Ergebnis ist also 4. Man spricht von „modularer Arithmetik“.
Der große Vorteil daran: Die modulare Exponentialfunktion kann man leicht ausrechnen, aber nur sehr schwer umkehren: Aus f(x) = xe lässt sich nur außerordentlich mühsam das x wieder bestimmen. Daher ist die Potenzfunktion ideal geeignet für die Public-Key-Kryptografie. Denn ein Entschlüsseln geht zwar, aber nur, wenn man den Schlüssel, die geheime Zahl d kennt. Dann ist es einfach, man potenziert das Ergebnis einfach mit d und erhält x.
Primzahlen spielen eine wichtige Rolle
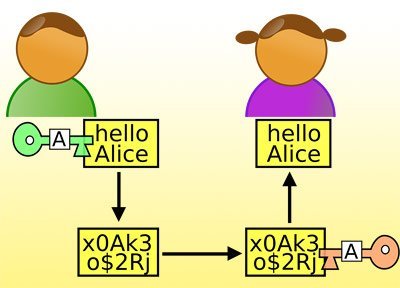
Beim RSA-Algorithmus wird die Nachricht zunächst in eine natürliche Zufallszahl (m) umgewandelt. Dann wendet er auf sie die modulare Potenzfunktion an, und zwar mit dem öffentlichen Exponenten e des Empfängers. Das kann jeder, denn dazu ist keinerlei Geheimnis notwendig. Entschlüsseln kann demgegenüber nur der legitime Empfänger, der seinen privaten Schlüssel d anwendet und damit die erhaltene Geheimbotschaft potenziert.
Jeder Teilnehmer, der eine Nachricht empfangen möchte (oder sein Computer), wählt zwei große verschiedene Primzahlen p und q und bildet ihr Produkt n = pq. Danach bestimmt er natürliche Zahlen e und d mit der Eigenschaft, dass ihr Produkt ed von der Form 1 plus ein Vielfaches von (p-1)(q-1) ist. Die Zahlen e und n werden veröffentlicht („öffentlicher Schlüssel“), die Zahl d dient als privater Schlüssel, den nur der Teilnehmer kennen darf. Die Primzahlen p und q müssen ebenfalls geheim gehalten werden.
Verschlüsselt wird so, dass die als Zahl dargestellte Nachricht m mit e modular potenziert wird: c =me mod n. Entschlüsselt wird mithilfe des privaten Schlüssels d = cd mod n. Ein vergleichsweise elementarer Satz des großen Mathematikers Leonhard Euler (1707–1783) garantiert, dass sich beim Entschlüsseln wieder die Nachricht m ergibt
Albrecht Beutelspacher (Universität Gießen / Mathematikum), DFG Forschung
Stand: 12.07.2013






