Es begann im Jahr 1200 mit einem Kaninchenpaar. Der Mathematiker Leonardo von Pisa, genannt Fibonacci, wollte eigentlich nur wissen, wieviele Nachkommen ein solches Pärchen langfristig produzieren kann. Sein Ziel war es dabei, eine mathematische Gesetzmäßigkeit zu finden, mit deren Hilfe sich das Fortpflanzungsverhalten auch im voraus berechnen ließe. Und er wurde fündig: Es zeigte sich, dass sich die Anzahl der Kaninchen wie eine Zahlenreihe verhielt, bei der immer die folgende Zahl die Summe der beiden vorangehenden bildete: 0,1,1,2,3,5,8,13,21,34,55,89,…
Inzwischen gehört diese so genannte Fibonacci-Reihe zum festen Inventar der Mathematik – aber nicht nur. Seltsamerweise findet sich diese Abfolge nicht nur in den abstrakten Zahlenspielen von Mathematikern, sondern auch in der Natur: Die Blätter der allermeisten Pflanzen entsprießen dem Stengel oder Stamm nicht zufällig verteilt, sondern bilden eine Spirale. Dabei steht das jeweils folgende Blatt immer um einen bestimmten Winkel gegen seinen Vorgänger versetzt.
Die Form der Spirale lässt sich durch Zahlenverhältnisse charakterisieren: Zählt man, wieviel mal man den Stengel von ersten Blatt umkreisen muss, bis man zu einem Blatt gelangt, dass genau über dem ersten steht, erhält man typischerweise die folgende Reihe von Brüchen: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/24,…. Das Erstaunliche: Sowohl in den Zählern als auch in den Nennern verbirgt sich die Fibonacci-Reihe. Und dies ist bei weitem nicht alles.
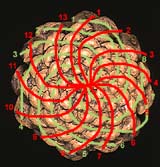
Fibonaccis Zahlenspiel findet sich auch in Blüten von Korbblütlern, in Disteln, Kakteen, den Köpfen von Blumen- oder Weißkohl, den Zapfen der Nadelbäume: Betrachten wir beispielsweise einen Tannenzapfen von oben, erkennt unser Auge unwillkürlich Verbindungslinien zwischen den einzelnen Samenanlagen, die sich, je nach Betrachtungsweise zu einem Satz linksdrehender oder rechtsdrehender Spiralen formen.