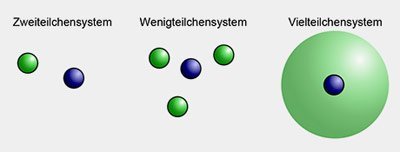
Ein Paar, ein Dutzend, eine Hand voll, ein Haufen: zahlreiche Sammelbegriffe existieren für verschiedene Mengen von Dingen. Manche davon sind fest definierte Zahlen, andere sind in ihrer Größe nur ungenau bestimmt. In der Physik ist bedeutend, ab welcher Anzahl von Atomen in einem System die physikalischen Regeln gelten, die sich dann auf ein beliebig großes System anwenden lassen. Entscheidend ist dabei der Übergang von einem System aus wenigen Einzelteilchen zu einem durch unendlich viele Teilchen beschriebenen System. Heidelberger Physikern ist es in Experimenten mit ultrakalten Atomen gelungen, einen solchen Übergang zu beobachten. Ihre Forschungsergebnisse veröffentlichten sie im Magazin „Science“.
Sorites-Paradoxon: Sandkörner zählen
Wie groß muss eine Ansammlung von Teilchen sein, damit die genaue Teilchenzahl unwichtig wird? Dieses physikalische Problem ist in der Philosophie als sogenanntes Sorites-Paradoxon bekannt. Im Mittelpunkt steht dabei die Frage, ab wann eine Ansammlung von Elementen einen ‚Haufen‘ bildet. Das Paradoxon wird häufig mit Hilfe von Sandkörnern verdeutlicht: Ein einzelnes Sandkorn ist eindeutig noch kein Haufen. Zwei ebenfalls noch nicht. Aber drei, oder fünf, oder doch erst zehn oder hundert? Umgekehrt stellt sich die Frage, wie viele Sandkörner man von einem Haufen entfernen muss, damit es kein Haufen, sondern nur noch eine Ansammlung weniger Einzelteilchen ist.
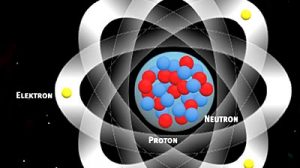
„Systeme, die aus vielen Teilchen bestehen, lassen sich in der Regel nur sehr schwer mikroskopisch exakt beschreiben. Wissenschaftler arbeiten daher häufig mit effektiven Theorien, mit denen nicht mehr die einzelnen Teilchen wie zum Beispiel Gasmoleküle in der Luft betrachtet werden, sondern makroskopische Größen wie Druck oder Temperatur“, erläutert Selim Jochim vom Max-Planck-Institut für Kernphysik.
Ausreichend viele Teilchen für Durchschnittswert
So beschreibt zum Beispiel die Temperatur die durchschnittliche Geschwindigkeit aller Teilchen im System, nicht die exakte Geschwindigkeit jedes einzelnen Teilchens. In einem komplexen System aus unendlich vielen Teilchen ist es unmöglich, jedem einzelnen Teilchen einen Wert zuzuweisen, der Durchschnitt muss zwingend verwendet werden. Bei nur zwei Teilchen dagegen liegt der Durchschnittswert genau dazwischen und beschreibt damit jedes der beiden Teilchen nur ungenau. Wie viele Teilchen muss ein System also enthalten, damit ein solcher Durchschnittswert das ganze System ausreichend genau beschreibt?