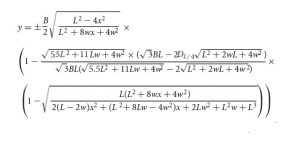Die Form eines Eis ist unverwechselbar – aber erst jetzt ist es Mathematikern gelungen, sie in einer universellen, für alle Eivarianten gültigen Formel zu erfassen. Dafür ergänzten sie die bisherigen Ansätze um eine weitere Gleichung, die den Grad des konischen Zulaufens am spitzen Ende beschreiben kann. Mithilfe dieser Formel lassen sich nun die Eiformen aller Vögel exakt berechnen, aber auch Materialien, Formen oder Gebäude in Eiform besser planen.
Das Ei ist eine nahezu perfekte Erfindung der Natur: Es bietet einem Embryo maximalen Platz, ist aber klein genug, um den Körper der Mutter zu passieren. Einmal gelegt, rollt es nicht weg und es ist so stabil, dass es selbst starken äußeren Belastungen standhält. Kein Wunder daher, dass das Ei seit der Zeit der Dinosaurier verbreitet ist. Und auch Technik und Architektur haben die Eiform schon als Vorbild genommen.
Vier Merkmale des Eis
Doch trotz seiner Bedeutung fehlte eines bisher: eine Universalformel, die alle Eigenschaften eines Eis perfekt beschreibt. Typischerweise werden vier geometrische Formen genutzt, um ein Ei zu beschreiben: der Kreis, die Ellipse, das Oval und das Pyriforme, das den Grad des konischen Zulaufens am spitzen Ende beschreibt. Gerade dieses Spitzzulaufen ist je nach Vogelart unterschiedliche stark ausgeprägt.
„Alle bisherigen Formeln haben das Problem, dass sie zwar eiähnliche Formen in Architektur und Kunst beschreiben können, aber nicht die Vielfalt echter Eier“, erklären Valeriy Narushin vom ukrainischen Umweltforschungsinstitut und seine britischen Kollegen. Zwar existieren für die geometrischen Formbestandteile Kreis, Ellipse und Oval mathematische Gleichungen, für das Pyriforme jedoch fehlte bislang eine passende Formel.
Eine Formel für alle Varianten
Das fehlende Element haben nun Narushin und seine Kollegen ergänzt. Sie haben eine Formel entwickelt, mit der sich alle Varianten der Eiform auf Grundlage von vier Messwetten beschreiben lassen: der Eilänge, der maximalen Breite, dem Abstand zwischen dem Bereich der maximalen Breite und der halben Länge des Eies und als viertem Wert dem Eidurchmesser einen Viertel der Eilänge vom spitzen Ende entfernt.
Setzt man diese Werte in die – ziemlich komplexe – Formel ein, lässt jedes beliebige Ei damit mathematisch beschreiben – egal wie rund, elliptisch oder birnenförmig es ist. Für ihre Studie haben Narushin dies bereits praktisch an den Eiern mehrerer Vogelarten mit möglichst unterschiedlichen Eiern überprüft – vom fast kreisrunden Ei der Uraleule über das ovale Ei des Emus bis hin zum extrem konisch zulaufenden Ei der Dickschnabellumme.
Vielseitig anwendbar
Es zeigte sich: Die mithilfe der neuen Formel gezeichneten Eiformen stimmten nahezu perfekt mit den realen Formen dieser Vogeleier überein. „Unsere Formel kann demnach theoretisch jedes Vogelei beschreiben, das in der Natur existiert“, schreiben die Forscher. „Damit haben wir erstmals eine universelle Gleichung für die Bestimmung der Eikonturen gefunden.“
Nach Ansicht der Wissenschaftler eröffnet diese Formel neue Möglichkeiten der Anwendung in den Biowissenschaften, der Agrarwissenschaft, der Technik, der Architektur und der Materialforschung. „Diese universelle Formel kann in einer ganzen Reihe fundamentaler Disziplinen genutzt werden“, so das Team.
„Die mathematische Gleichung unterstreicht die fast philosophische Harmonie zwischen Mathematik und Biologie und von diesen ausgehend bringt sie sogar ein tieferes Verständnis unseres Universums – alles in der Form eines Eis“, konstatiert Koautor Michael Romanov von der University of Kent. (Annals of the New York Academy of Sciences, 2021; doi: 10.1111/nyas.14680)
Quelle: University of Kent
