Eine im Jahr 1985 aufgestellte mathematische Vermutung – die Andrews-Robbins-Vermutung – haben österreichische Mathematiker jetzt erstmals bewiesen. Die jetzt in den “Proceedings of the National Academy of Sciences” (PNAS) veröffentlichte Beweisführung gelang nur unter Einsatz enormer Computer-Ressourcen und erst nach computergerechter Aufbereitung der Formel. Mit dem Beweis wird bestätigt, dass sich die Struktur so genannter „total symmetrischer planarer Partitionen“ mit einer einzigen Formel beschreiben lässt. Gleichzeitig ist damit auch die letzte einer ganzen Reihe berühmter mathematischer Vermutungen bewiesen, die sich auf planare Partitionen beziehen.
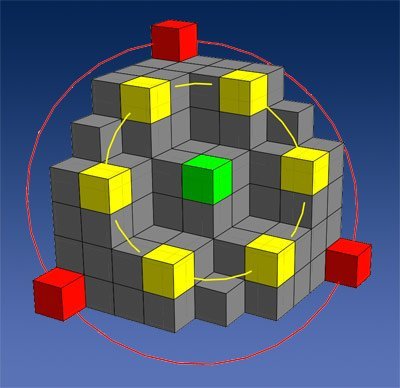
Auch Mathematiker spielen mit Bauklötzen. Zumindest dann, wenn ihr Interesse so genannten planaren Partitionen gilt. Denn diese werden durch Türme von „Bauklötzen“ auf einer schachbrettartigen Grundfläche dargestellt. Bauen Mathematiker nun solche planaren Partitionen, müssen sie bestimmten Regeln folgen: Kein Turm darf höher sein, als die Grundfläche breit ist, und als ein anderer Turm dahinter oder links. Die Frage, wie viele verschiedene Anordnungen von Türmen sich bei einer gegebenen Grundflächengröße bauen lassen, ist dank einer entsprechenden Formel leicht beantwortet.
Stimmt die Formel?
Schwieriger wird es, wenn die Anordnungen der Türme bestimmte Symmetrien aufweisen sollen oder wenn man nicht die Anordnungen selbst, sondern ihre Bestandteile abzählen will. Zwar gibt es auch dafür Formeln. Doch die Krux ist – nicht bei allen diesen Formeln weiß man, ob sie wirklich korrekt sind. Das wird nur vermutet. Der Beweis, dass eine bestimmte dieser Formeln korrekt ist, gelang nun Christoph Koutschan und Manuel Kauers vom Institut für Symbolisches Rechnen der Johannes Kepler Universität Linz in Zusammenarbeit mit Professor Doron Zeilberger aus den USA. Dabei ging es um eine Formel für die Berechnung einzelner Komponenten in total symmetrischen planaren Partitionen.
Hilfsgleichung würde eine Million DINA4-Seiten füllen
„Wir haben es den Computer machen lassen“, erklärt Koutschan die Methode der Beweisführung. „In manchen Bereichen der Mathematik ist das ja inzwischen Routine.“ Das Prinzip hinter solchen Computerbeweisen ist zunächst einfach. Um A=B zu beweisen, berechnet der Computer eine Hilfsgleichung U=V mit folgenden zwei Eigenschaften: „Wenn U=V wahr ist, dann ist auch A=B wahr“
und „ob U=V wahr ist, kann leicht überprüft werden“.
Was so leicht klingt, stellte tatsächlich eine große Herausforderung dar, wie Koutschan weiter ausführt: „Dieses Verfahren funktioniert nicht für jede Gleichung. Unser wesentlicher Schritt war es, die Andrews-Robbins-Vermutung in eine geeignete Form zu bringen, die dann mit dem Computer bewiesen werden konnte.“ Dass die Hilfsgleichung dabei in Wirklichkeit etwas komplexer als „U=V“ war, belegt ihr Umfang: Ausgedruckt würde sie rund eine Million A4-Seiten bedecken und ist damit vermutlich die längste Gleichung, die je in einem mathematischen Beweis verwendet wurde.
Der letzte Beweis auf Stanleys Liste
Der Aufwand für diese Formulierung hat sich jedoch gelohnt. Denn mit dem Beweis der Andrews-Robbins-Vermutung gelang es den Forschern, die letzte einer Reihe berühmter Vermutungen zu beweisen. Diese wurden im Jahr 1985 vom US-Mathematiker Richard Stanley auf einer historischen Konferenz in Montreal vorgestellt. Alle diese Vermutungen wurden in den folgenden Jahren bewiesen – bis auf die Andrews-Robbins-Vermutung.
„Als letzter verbleibender Eintrag in Stanleys Liste hat diese Vermutung viele bedeutende Experten und Expertinnen angezogen“, so Kauers. „Trotzdem blieb sie für fast 30 Jahre unbewiesen. Dass der Beweis schließlich mit einem automatischen Beweisverfahren gelungen ist, zeigt, dass moderne Computerprogramme mathematische Probleme knacken können, an denen traditionelle Mathematiker und Mathematikerinnen scheitern.“ Zwar sind solche Erfolge bisher die Ausnahme, doch zeigt dieses Projekt das Potenzial einer computerbasierten Beweisführung. Vor dem Hintergrund des rasanten Fortschritts der Rechnerleistung werden Computer vielleicht eines Tages sogar Antworten zu den größten offenen Fragen der Mathematik liefern. (PNAS, 2011; DOI: 10.1073/pnas.1019186108)
(Universität Linz / PR&D, 26.01.2011 – NPO)