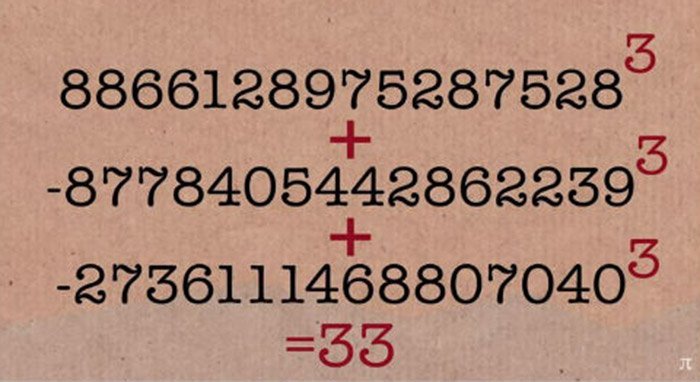Mathematik: Rätsel der 33 geknackt

Vertracktes Zahlenspiel: Ein britischer Mathematiker hat ein jahrzehntealtes Rätsel gelöst – die Frage, ob und wie sich die Zahl 33 als Summe dreier Kubikpotenzen ausdrücken lässt. Die 33 war eine von nur zwei Zahlen unter 100, für die es noch keine Lösung dieser sogenannten Diophantischen Gleichung gab. Jetzt bleibt nur noch die Zahl 42 – Fans von Douglas Adams‘ „Per Anhalter durch die Galaxis“ ahnen vermutlich warum.

In der Mathematik gibt es eine ganze Reihe ungelöster Fragen, die ganz eng mit scheinbar simplen Zahlen oder Alltagsphänomenen verknüpft sind. So ist bei den Primzahlen noch immer nicht bewiesen, ob es wirklich unendlich viele sogenannter Primzahlzwillinge gibt. Bei der Kreiszahl Pi rätseln Mathematiker, ob ihre Ziffernfolge mathematisch normal ist. Und die scheinbar triviale Frage, wie sich Kugeln am dichtesten packen lassen, wurde erst 2017 bewiesen – 400 Jahre nachdem Johannes Kepler eine Lösung vorschlug.

Summe aus drei Kubikpotenzen

Eine weitere unbeantwortete Frage der Mathematik ist, ob sich alle ganzen Zahlen als Summe aus drei Kubikpotenzenn beschreiben lassen. Nimmt man die Zahl acht wäre die Lösung beispielsweise 2³ + 1³ + -1³. Schon seit den 1950er Jahren versuchen Mathematiker, diese Unterform der sogenannten Diophantischen Gleichungen für alle ganzen Zahlen zu lösen.

Inzwischen ist zumindest schon klar, dass es nicht für alle ganzen Zahlen eine Lösung gibt: Zahlen, bei denen durch 9 geteilt ein Rest von 4 oder 5 bleibt, sind nicht durch drei Kubikpotenzen darstellbar. Allein im Zahlenraum bis 100 scheiden damit 22 Zahlen aus. Von den 78 verbleibende haben Mathematiker bisher für 76 Zahlen eine Kubikpotenz-Kombination gefunden. Zwei aber blieben offen: 42 und 33.

Gleichung für die 33 geknackt

Jetzt hat Andrew Booker von der University of Bristol für die 33 die Lösung gefunden. Auf die Idee kam er, nachdem er ein YouTube-Video zur ungelösten Potenzfrage der Zahl 33 gesehen hatte. „Danach wollte ich es unbedingt selbst versuchen“, sagt Booker. Um die Gleichung zu knacken, entwickelte er ein Computerprogramm, das systematisch nach Kubikpotenz-Lösungen für Zahlen bis 1.000 suchte.

Nach einigen Wochen Rechenzeit wurde das Programm fündig. Zur Freude und Überraschung des Mathematikers hatte sein Algorithmus ausgerechnet die lange gesuchte 33 geknackt. „Ich war fast sicher, dass irgendwo unter den Zahlen bis 1.000 fündig werden würde – aber dass es die Zahl 33 werden würde, habe ich nicht gedacht“, so Booker. Die 33 hat einen besonderen Stellenwert, weil sie die kleinste Zahl ist, für die diese Gleichung bisher nicht gefunden war.

Es bleibt: 42

Jetzt ist klar: Es gibt eine Lösung und sie lautet: 33 = (8,866,128,975,287,528) ³ + (–8,778,405,442,862,239) ³ + (–2,736,111,468,807,040) ³. „Ich bin vor Freude in die Luft gesprungen, als ich das geknackt hatte“, sagt Booker. Damit bleibt im Zahlenraum unter 100 nur noch eine einzige Zahl, für die die Diophantische Gleichung nicht gelöst ist: 42.

Science-Fiction-Fans dürfte dies nicht wundern: In Douglas Adams‘ Romanreihe „Per Anhalter durch die Galaxis“ spielt die Zahl 42 eine entscheidende Rolle. Denn sie ist die Antwort auf die Frage nach „Life, the Universe and Everything“.

Quelle: University of Bristol