Worthäufigkeiten als Hyperbel: Forscher haben eine weitere mathematische Gesetzmäßigkeit in literarischen Werken entdeckt. Wie oft ein Wort im Text auftaucht und in welchem Verhältnis es zum nächsthäufigen steht, lässt sich demnach mit einer verblüffend einfachen Formel ausdrücken. Übereinstimmungen mit diesem Zipfschen Gesetz fanden die Wissenschaftler immerhin in knapp der Hälfte der gut 30.000 englischsprachigen Werke im Projekt Gutenberg.
Dass sich in Literatur durchaus mathematische Prinzipien verstecken können, hat erst vor kurzem die Entdeckung von fraktalen Strukturen in großen Werken der Weltliteratur bewiesen. Aber es gibt noch viel vordergründigere Mathematik in geschriebenen Texten: das Zipfsche Gesetz. Diese 1930 vom US-Linguisten George Zipf aufgestellte Regel besagt, dass die Häufigkeit bestimmter Wörter in einem Text einer verblüffend simplen mathematischen Funktion folgt.
Worthäufigkeit als Hyperbel
Nach dem Zipfschen Gesetz entspricht die Verteilung der Worthäufigkeiten dabei in ihrer einfachsten Form einer Hyperbel mit der Formel 1/n. Konkret gesagt: Das häufigste Wort in einem Text kommt genau doppelt so oft vor wie das zweithäufigste, dieses wiederum ist ein dreimal häufiger als das drittplatzierte und so weiter. Für einzelne Werke wie beispielsweise den Roman Effi Briest von Fontane haben Analysen diesen Zusammenhang auch schon bestätigt.
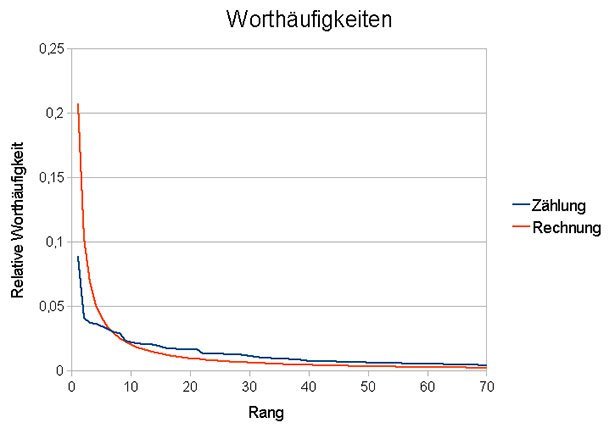
Aber gilt das Zipfsche Gesetz für alle literarischen Werke? Um das herauszufinden, haben Forscher der Universität Autònoma de Barcelona erstmals alle englischsprachigen Werke im Gutenberg-Projekt auf ihre Übereinstimmung mit drei Varianten dieses mathematischen Gesetzes untersucht. 30.000 Werke, und damit so viel wie noch nie zuvor, testeten die Wissenschaftler dafür.
Gut Übereinstimmung bei 40 bis 55 Prozent
Das Ergebnis: Werden alle Wörter berücksichtigt, folgen immerhin rund 40 Prozent der literarischen Werke der simpelsten Formulierung des Zipfschen Gesetzes. Ließen die Forscher jeweils die Wörter weg, die nur einmal im gesamten Buch vorkamen, verbesserte sich dieser Anteil auf 55 Prozent.
„Es ist ziemlich überraschend, dass die Worthäufigkeit in so vielen Werken einer so einfachen, nur durch einen Parameter bestimmten Formel folgt“, konstatiert Studienleiter Alvaro Corral. „Obwohl Literatur als einer der Ausdrucksformen mit der größten kreativen Freiheit gilt, können nicht einmal William Shakespeare oder Charles Dickens der Tyrannei des Zipfschen Gesetzen entkommen.“
Zipf-Variante von der Sprache abhängig?
Wie die Forscher betonen, war es gar nicht ihr Ziel, dass ihre Zipf-Varianten auf so viele Texte wie möglich passen – eher im Gegenteil. Sie wählten bewusst eher strenge Rahmenbedingungen aus. „Es ist daher erstaunlich, wie gut die einfachste Zipf-Verteilung bei einer so großen Menge an Texten funktioniert“, betonen die Wissenschaftler.
Die anderen beiden, etwas komplexeren Varianten des Zipfschen Gesetzes passten allerdings weniger gut auf die Texte. Nach Ansicht der Forscher könnte dies mit der englischen Sprache zusammenhängen. Weil im Englischen relativ wenige Wörter explizite Beugungsformen besitzen, gibt es weniger Wörter mit geringen Häufigkeiten als in anderen Sprachen, vermuten sie. Ob bei diesen möglicherweise eine andere Zipf-Variante besser passt, müssen weitere Studien klären.
Ein bisschen Zipf steckt überall
Übrigens: Das Zipfsche Gesetz ist keineswegs auf Literatur beschränkt, ganz im Gegenteil. Es verbirgt sich in so unterschiedlichen Bereichen wie den Tönen in einem Musikstück, bei den Besuchern einer Website, oder den Mitarbeitern von Firmen. Sogar in der Häufigkeit der Proteine in unseren Körperzellen findet sich dieses mathematische Gesetz wieder.
„Versuche, dafür eine Erklärung zu finden, hat es schon viele gegeben“, sagen Isabel Moreno-Sánchez und ihre Kollegen. „Aber bisher konnte man sich auf keine gültige Lösung einigen.“ Sie sehen in den neuen Möglichkeiten der Analyse großer Datenmengen eine Chance, hier künftig einen Schritt weiter zu kommen. (PLSO ONE, 2016; doi: 10.1371/journal.pone.0147073)
(Universitat Autònoma de Barcelona, 24.02.2016 – NPO)
