Drohendes Quantenchaos: Forscher haben untersucht, wie gut die Quantencomputer von IBM, Google und Co das fragile Gleichgewicht zwischen nötiger Kopplung und unerwünschten Resonanzen meistern. Denn wenn die Balance der Quantenbits kippt, droht ein unkontrolliertes Quantenchaos und damit ein Kollaps der Rechenfähigkeit. Das Ergebnis: Die Architektur von IBM könnte anfälliger für einen solchen Kollaps sein – vor allem, wenn die Systeme künftig auf mehr Qubits erweitert werden.
Quantencomputer sind im Kommen, längst liefern sich Firmen wie IBM, Google und Co einen Wettlauf um die leistungsfähigsten Quantenrechner. Ihre bisher 117 Qubits beziehungsweise 64 Qubits umfassenden Systeme beruhen auf quantenphysikalischen Interaktionen von Ladungsinseln in supraleitenden Materialien. Damit diese sogenannten Transmon-Qubits Rechenoperationen durchführen können, müssen sie einerseits möglichst ungestört und gut abgeschirmt im Überlagerungszustand bleiben. Andererseits jedoch müssen die Qubits miteinander gekoppelt werden, um Schaltkreise zu bilden.
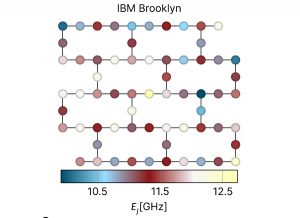
Fragile Balance
Doch genau darin liegt ein Problem: Die gängigen Quantencomputer arbeiten in einem fragilen Gleichgewicht zwischen Ordnung und Unordnung. Die miteinander gekoppelten Quantenbits ähneln einem System gekoppelter Pendel, dessen Fluktuationen sich leicht zu unkontrollierbar großen Schwingungen mit katastrophalen Folgen aufschaukeln können – ähnlich wie bei einer Brücke, die von einer Menschengruppe im Gleichschritt überquert wird.
„Der Transmon-Chip toleriert nicht nur, sondern benötigt sogar effektiv zufällige Qubit-zu-Qubit-Unvollkommenheiten“, erklärt Erstautor Christoph Berke von der Universität zu Köln. Die zurzeit gängigen Quantencomputersysteme nutzen dafür unterschiedliche Methoden. IBM platziert Qubits alternierend im Gitter, um unerwünschte Kopplungen zwischen gleichen Nachbarn zu verhindern. Die Quantencomputer der TU Delft und von Google hingegen nutzen aktiv eingeführte lokale Störungen, um unerwünschte Resonanzen zu blockieren.
Gefährlich nahe am unkontrollierten Chaos
Wie gut diese verschiedenen Methoden funktionieren, haben nun Berke und seine Kollegen mithilfe von drei verschiedenen Techniken untersucht. „In unserer Studie gehen wir der Frage nach, wie zuverlässig das Prinzip ‚Stabilität durch Zufall‘ in der Praxis ist“, so Berke. Dabei ergaben die Tests eine unerwartete Erkenntnis: Schon vor dem Kollaps gibt es eine überraschend ausgedehnte Grauzone, in der unerwünschte Resonanzen die Quantenzustände zwar schon beeinträchtigen, aber die Schwelle zum „harten Quantenchaos“ noch nicht überschritten ist.
Zum anderen zeigte sich: Einige der kommerziellen Systemarchitekturen bewegen sich gefährlich nahe an der Instabilität, so das Team. „Als wir die Google- mit den IBM-Chips verglichen, stellten wir fest, dass im letzteren Fall die Qubit-Zustände so weit gekoppelt sein könnten, dass kontrollierte Rechenoperationen beeinträchtigt werden können“, berichtet Berkes Kollege Simon Trebst. Das System dieser Rechnerarchitektur sei nahe an einer Phase unkontrollierbarer chaotischer Fluktuationen.
Probleme bei der Skalierung auf mehr Qubits
Bedeutung haben diese Erkenntnisse vor allem für die nötige Skalierung der Quantencomputer auf Systeme mit mehr Qubits. Denn für viele Anwendungen sind die jetzigen Quantenrechner noch nicht geeignet. Doch genau diese Erweiterung könnte das schon jetzt fragile Gleichgewicht beispielsweise der IBM-Rechner kippen lassen: „Wir würden so weit gehen, zu spekulieren, dass dieses System die Generalisierung zu größeren und zweidimensional verbundenen Array-Geometrien, wie sie für komplexere Anwendungen nötig sind, nicht tragen kann“, schreiben die Forscher.
Seniorautor David DiVincenzo von der RWTH Aachen ergänzt: „Unsere Studie zeigt, wie wichtig es für Hardware-Entwickler ist, die Modellierung von Bauelementen mit modernster Quantenzufallsmethodik zu kombinieren und die ‚Chaos-Diagnose‘ als Routinebestandteil in das Design von Qubit-Prozessoren auf der supraleitenden Plattform zu integrieren.“ (Nature Communications, 2022; doi: 10.1038/s41467-022-29940-y)
Quelle: Universität zu Köln
