In der Welt der Quanten können kleinste Teilchen selbst Barrieren durchdringen – sie „tunneln“ hindurch. Weil dieser seltsame Effekt in unserer Makrowelt nicht vorkommt und er zudem schwer genau zu messen ist, war bisher unklar, ob ein Quantenteilchen für diese Passage Zeit benötigt oder nicht. Eine theoretische Studie spricht nun für ersteres und zeigt auf, wie sich dies im Experiment nachweisen ließe.
In der Welt der kleinsten Teilchen gelten andere Gesetze als in unserer Makrowelt. Anders als ein Fußball, der von einer Mauer mit 100-prozentiger Wahrscheinlichkeit abprallt, hat daher ein Quantenteilchen eine kleine Chance, eine Barriere zu durchdringen – und dies selbst wenn seine Energie dafür eigentlich nicht ausreicht. Durch dieses sogenannte Tunneln kann beispielsweise ein Elektron dem von der Anziehungskraft des positiv geladenen Atomkerns gebildeten Käfig entkommen. Es existiert daher eine gewisse Wahrscheinlichkeit, ein solches Elektron jenseits des sogenannten Potenzialwalls zu finden. Wie schnell dieses Tunneln erfolgt und ob es vielleicht sogar instantan stattfindet, war bisher unklar.
Auch das Tunneln braucht Zeit
Forscher des Max-Planck-Instituts für Kernphysik in Heidelberg belegen nun in ihrer theoretischen Studie, dass das Elektron tatsächlich eine kurze, aber messbare Zeit in der Barriere verbringt. „Unsere Studie gibt Hinweise, wie sich die Eisenbud-Wigner-Smith-Zeit, die das Elektron in der Tunnelbarriere verbringt, messen lässt“, erklärt Studienleiter Christoph Keitel. Wo und wie Messungen aussagekräftiger werden, leiten die Forscher aus einer theoretischen Betrachtung des Tunnelprozesses ab, in der sie erstmals sogenannte relativistische Effekte berücksichtigten. Diese treten auf, wenn der Atomkern und die elektromagnetische Kraft eines intensiven Lasers das tunnelnde Elektron fast auf Lichtgeschwindigkeit beschleunigen.
„Wir haben bewiesen, dass das Bild des Tunnelns auch für Elektronen, die fast auf Lichtgeschwindigkeit beschleunigt wurden, noch zutrifft“, sagt Michael Klaiber, der am Heidelberger Max-Planck-Institut einen Großteil der Rechnungen vorgenommen hat. Selbstverständlich ist das nicht, weil die Vorstellung eines Elektrons, das durch eine Potenzial-Barriere tunnelt, nur die elektrische Komponente des elektromagnetischen Laserfeldes berücksichtigt. Relativistische Elektronen nehmen dagegen auch die magnetische Komponente des Lichts wahr, die senkrecht zum elektrischen Feld steht. Damit folgen die Elektronen während des Tunnelns sowohl den Gesetzen der Quantenmechanik als auch denen der Relativitätstheorie.
Verschiebung als Zeitanzeiger
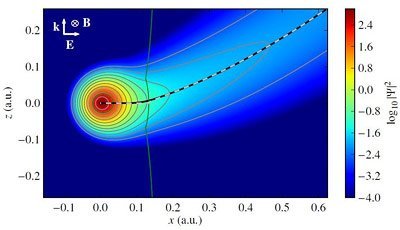
„Das magnetische Feld des Lasers übt dann auf das Elektron die Lorentzkraft aus, die das Elektron auf seinem Weg durch die Barriere leicht verschiebt und auch seinen Impuls verändert“, erklärt Klaiber. Das Elektron verlässt die Barriere daher an einer etwas anderen Stelle, als ohne das Magnetfeld zu erwarten wäre. „Wie weit das Elektron in der Barriere abgelenkt wird, hängt dann von der Stärke des Magnetfeldes und der Dauer des Tunnelprozesses ab.“ Aus dieser Verschiebung konnten die Forscher berechnen, wie schnell das Elektron durch den Tunnel saust.
Dabei kommen sie zu dem Ergebnis, dass das Elektron theoretisch mit bis zu 70 Prozent der Lichtgeschwindigkeit durch die verbotene Zone fliegt, während es außerhalb der Barriere nur mit einigen Prozent der Lichtgeschwindigkeit startet. Dieses Resultat mit einem Experiment zu überprüfen, ist jedoch knifflig. Denn um die Verschiebung des Tunnelausgangs und somit die Tunnelzeit zu messen, müsste man Ort und Impuls des Elektrons direkt an der Barriere messen. Das ist praktisch nicht möglich. Mindestens ein paar Zentimeter Abstand braucht ein Detektor zum Atom.
Nahe der Kuppe statt am Fuß des Walls
Doch die Heidelberger Forscher warten mit einer Lösung für dieses Problem auf. Ihren Rechnungen zufolge verwischt der Effekt, den das Magnetfeld auf das tunnelnde Elektron ausübt, nämlich nur, wenn es durch eine lineare, also gleichmäßig steile Barriere tunnelt. Doch der Potenzialwall um einen Atomkern ist in etwa so geformt wie ein Erdwall: Seine Flanken sind gleichmäßig steil, während seine Kuppe sich bis zum Scheitelpunkt auf beiden Seiten allmählich abflacht. „Statt wie bisher den Tunnelprozess am Fuß des Walls zu beobachten, sollte man ihn nah an der Kuppe messen“, sagt Klaiber.
Das ließe sich machen, wenn Experimentatoren einem Elektron mit Laserlicht geeigneter Farbe einen Energieschubs verpassen, der es bis knapp unter den Scheitelpunkt der Barriere befördert. Dann ist es jedoch diffizil, die Elektronen, die so nah an der Kuppe durch den Potenzialwall tunneln, von denjenigen zu unterscheiden, die einfach über die Barriere fliegen. Um den Anteil der tunnelnden Elektronen zu erhöhen, müssen Experimentatoren mit sehr kurzen Pulsen arbeiten, was die Versuche aufwendiger macht. Jedenfalls könnten sie dann den Weg eines Elektrons von ihren Detektoren aus bis zum Tunnelausgang zurückverfolgen. Aus der Verschiebung des Ausgangs ließe sich berechnen, wie lange sich das Teilchen dank der Quantenmechanik dort aufhalten konnte, wo es nach dem Bild der klassischen, nicht quantenmechanischen Physik gar nicht sein darf. (Physical Review Letters, in press; arXiv:1205.2004v2 )
(Max-Planck-Gesellschaft, 19.04.2013 – NPO)